扇形の面積

どうもタジモブログです。

以前、正方形に内接する円の面積という記事を投稿しました。またまた面積の問題で面白い問題があったので、それを投稿します。前回同様、下の息子が、私立中学を目指していて、その勉強で出会った問題となります。

1.問題

下のような図形があって、最終的には、斜線部分の面積を求める問題となります。円周率は3.14となっています。角OEA=角OBD=90°です。

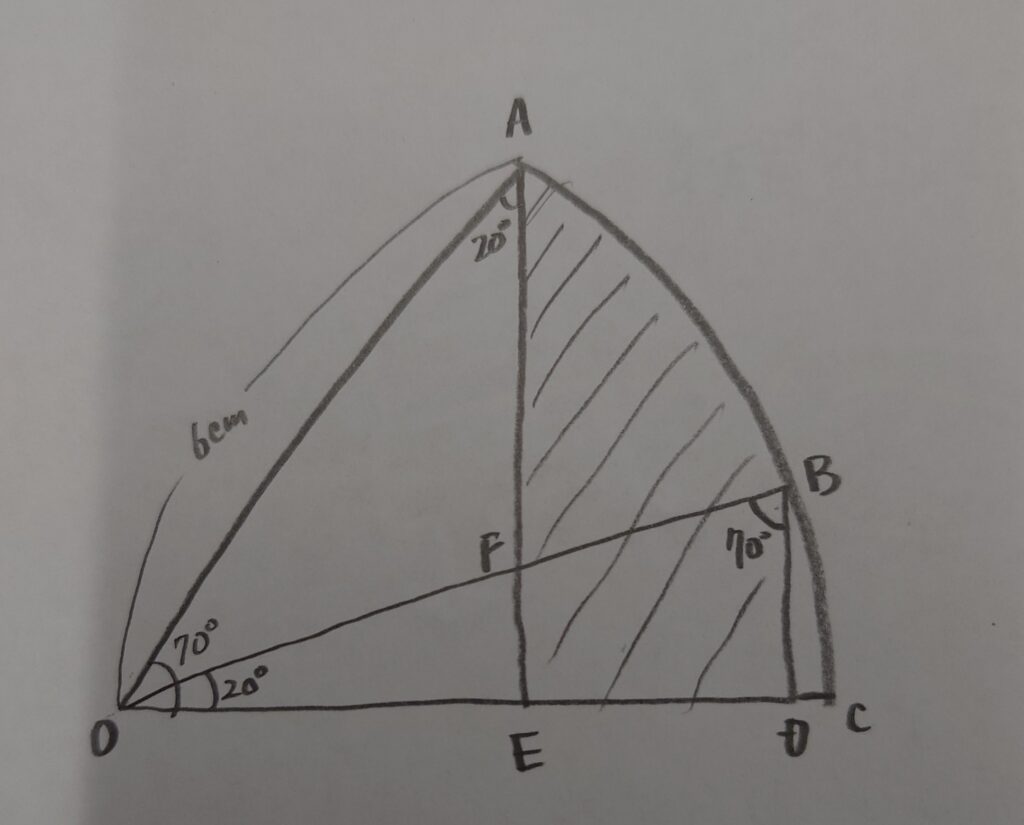
1.1 (1)　扇形の面積

まず初めに求めるのは、扇形OACの面積です。これは簡単で、角度が70°とわかっているので、

円周率×半径×半径×角度÷360で求まります。

3.14×6×6×70÷360

=21.98cm²

1.2 (2)　△OAEと合同な三角形は？

次に求めるのは、△OAEと合同な三角形です。角が対応するように書きなさいという指定があります。ぱっと見で△BODと分かりますが、一応理由を書きます。辺BOが円の半径にあたるため、6cmとなります。また、辺BOの両隣の角度は70°と20°となります。一辺とその両隣の角度が等しいため、△OAEと△BODが合同となります。

1.3 (3) 　斜線の面積は?

さて、(1)と(2)を経てやっと斜線の面積を求める問題にたどり着きました。分割してある部分の面積を下のように、アイウエとおきます。

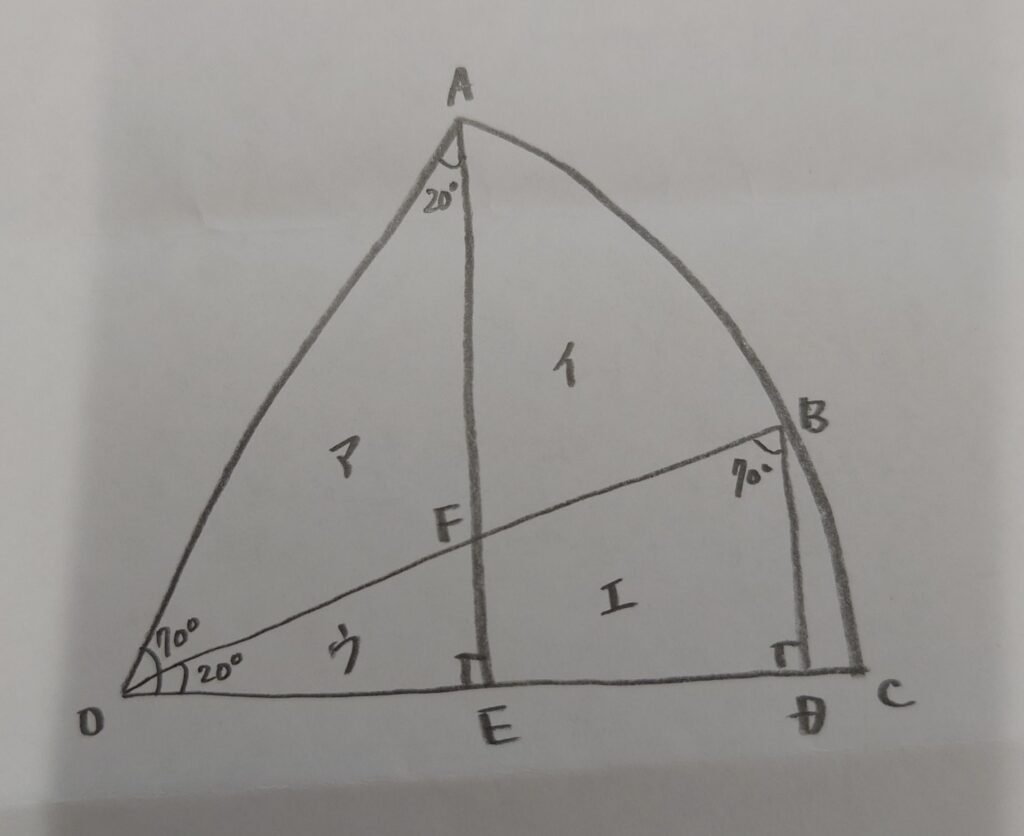
(2)で求めたように△OAEと△BODは合同なため、アとエの面積は同一になることがわかります。

従いまして、斜線部分は、アとイ部分の扇型の面積になります。これは、角度が分かっているので、最初に出てきた公式を使って、次のように求めることができます。

3.14×6×6×50÷360

=15.7cm²

【別解】

さて、(1)で求めた答えも使って、斜線以外部分の面積を引く、という方法で無理やり解くこともできます。

まず、△OAEの面積を□とおきます。△OAEと△BODは合同なため、△BODの面積も□となります。従って、下の図におけるBDC部分は扇形OCB-□とすることができます。扇形OCBの面積は、

3.14×6×6×20÷360

=6.28cm²

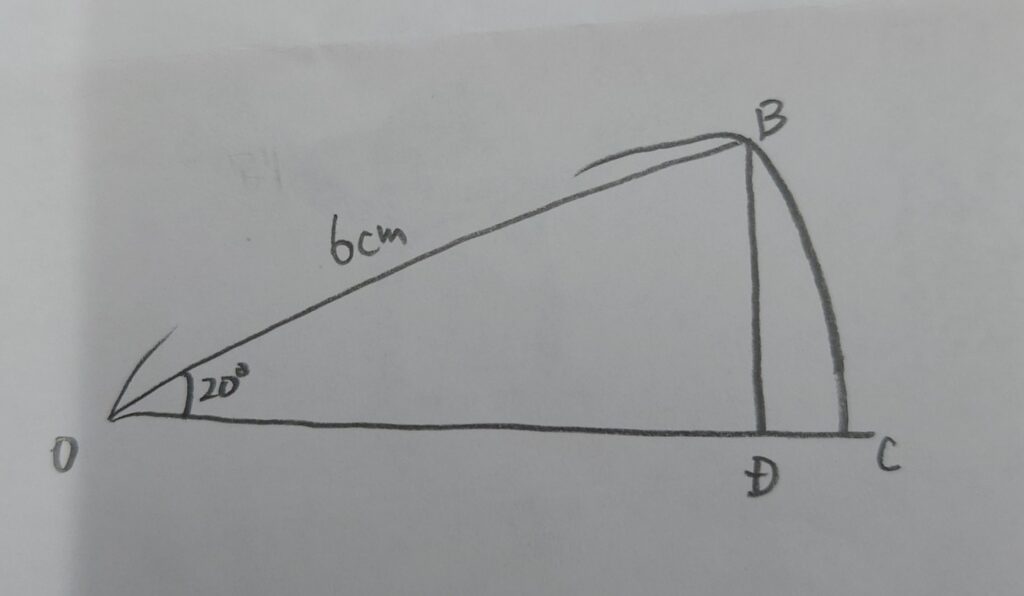
斜線部分の面積は、(1)の答えから、△OAEとBDC部分の面積を引けばいいので、

21.98-□-(6.28-□)

=21.98-6.28

=15.7cm²

（□が消えるというのがポイントです）

前の記事のように面積を□と置いてしまっているのが、小学生の問題でいいのかという疑問は残りつつ使っています。

2. さいごに

小学生が解く問題ではありますが、大人が解いてもパズルみたいで楽しいですね。これからも、このような問題にであったら紹介していきたいと思います。