正方形に内接する円の面積

どうもタジモブログです。

私には中学受験をして中高一貫の私立を目指している子供がいるのですが、算数の塾の宿題を教えていたら、こんな問題があったので、その解き方の記事となります。面白い問題ではあるのですが、今どきの小学生はこんな難しい問題を解くのだと感心もしましたが、このような問題を解けないと、私立の中学校にはいけないのだなぁと感じました。がんばれ息子よ！また、同じような境遇のお父さん、お母さんの一助になればとも思います。やっぱり、塾で習うのもいいですが、家庭での勉強も大事だと思いますので、少しでも勉強の足しになればいいと感じています。

1.問題

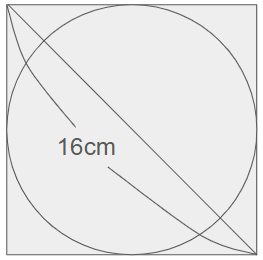
上の図のように正方形とその中に円があり、正方形の対角の長さは16cmです。(円周率は3.14とします。)

（1）正方形の面積を求めましょう

（2）円の面積を求めましょう

2.(1)の解き方

下の図のように、もう一本の対角線を引きます。正方形の角をABCD、円の中心・対角線どおしの交点をOと名前をつけます。

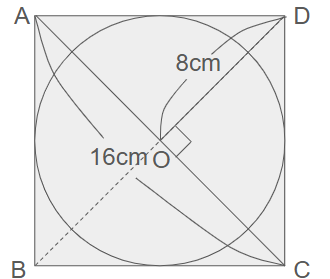
すると正方形の対角線どおしなので、直角に交わります。また、正方形の対角線どおしなので、ODの長さは対角線の半分の長さとなるので、図のように8cmになります。

したがって、三角形ACDの面積は、下底×高さ÷2なので、

16cm×8cm÷2=64cm²

となります。正方形の面積はこの面積の2倍となるので、

64cm2×2=128cm²

これが(1)の答えとなります。

3.(2)の解き方

円の半径=正方形の一辺の長さの半分を□cmと置きます。

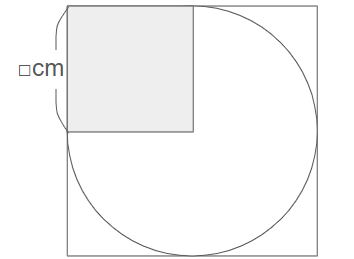
(1)の答えから、色を塗った部分の面積は(1)の4分の1になるため、

□cm×□cm＝128cm2÷4

□cm×□cm=32cm²・・・①

となります。

円の面積は、半径×半径×3.14なので、求めたい円の面積は、

□cm×□cm×3.14

となり、①を用いて、

32cm²×3.14=100.48cm²

となります。

4.おわりに

小学生の問題なのに、一辺の長さを□と置くこと（中学生だとxにしたりするのかな？）が正しいのかな？と思ったりするのですが、答えを見るとそうやっているので、何とか理解できる範囲なのかなと思います。公文の中学校入試では、ひたすら計算で微分積分もやったりするらしいので、どこまでが範囲とかは無いのでしょうね。

算数の問題ではなく、ひらめきを必要とするパズルのようで面白いですね。